QAM (pronounced “kwom”) stands for Quadrature Amplitude Modulation. It is a way of modulating, or changing, a waveform, called a carrier wave, to encode some sort of information. In the case of 802.11, this information would be the 1’s and 0’s that make up the data you wish to transmit across the RF (Radio Frequency) medium.
This is done by manipulating the phase and amplitude of the carrier wave. The number of possible phase/amplitude combinations is dependent upon the type of QAM being used (e.g., 4-QAM, 16-QAM, etc.). These phase/amplitude combinations are called symbols. Each symbol is sent for some uniform length of time, or symbol period, and can represent two or more bits of data.
QAM does this by basically taking two sinusoid waves of the same frequency that are in quadrature and adding them together.
What does that mean?
Well, a sinusoid is simply a smooth, continuous wave—like the sine and cosine waves that you may have learned about in Math class. In fact, sine and cosine waves are two sinusoids that are 90 degrees out of phase with each other. One full cycle of a wave is considered to be 360°, so sine and cosine waves are basically two waveforms with the same frequency but offset by a quarter of their wavelength (i.e. 90°).
If you were to draw a sine wave and a cosine wave, you would draw the same basic shape for each, but they would each appear to have different origins, or starting points.
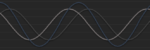
See the image below. The sine wave is in red, and the cosine is green.

Notice how, when starting the curve at 0°, the red curve resembles a sine wave, but if you look at the same curve as originating at 90°, it looks like a cosine wave. They are both identical, but with different starting points.
Why Am I telling you this?
Well, when two waves are 90 degrees out of phase, we say they are in quadrature. We could also say that these two waves are orthogonal to each other, which could also refer to the 90° offset, but orthogonality also implies that these two waves are discrete, unrelated, independent components that will not interfere with one another, i.e. changing one does not affect the other. When these two signals are eventually summed and transmitted, this property of orthogonality is what allows the receiver to isolate and recover the individual component waves from the combined signal.
Orthogonality will really come into play when we discuss OFDM (Orthogonal Frequency Division Multiplexing) in a future article. OFDM involves the combining (or multiplexing) of many subcarriers (i.e. component waves) before transmission.
In QAM, we usually refer to one of these waves as the I, or “In-Phase” component, and the other as the Q, or “Quadrature” component. Here, we will consider the cosine wave to be the I component and the sine wave to be the Q component.
Now, when we take I and Q signals of the same amplitude, and add them together, the resultant wave will have a phase directly between the phases of the I and Q signals. You can see this in the image below, where we are adding the I and Q waves together. You can see the resultant wave in blue with a phase of 45 degrees—exactly between 0° (the I signal) and 90° (the Q signal).

Now, before we go on, I would like to say a few words about “phase.” The phase of a wave indicates the location of some specific point in the wave cycle. It is expressed as an angle, usually in degrees (but, you could also use radians). For our purposes, when we mention “phase,” we usually don’t mean the absolute phase just described, but the phase difference between similar points on two waves. Accordingly, when we speak of a wave having a certain phase, it’s almost always in reference to another wave. So, in the above image, the resultant wave has a phase of 45° in reference to the In-Phase wave, or I component.
It may be confusing that we call the I component, “In-Phase.” In-Phase to what? Well, it has to be called something, but really, think of it more as the reference point for the Quadrature (Q) wave.
We can invert (shift by 180°) either, or both, of these waves while still maintaining orthogonality. This will give us 4 different possible combinations. For example, if we invert the I signal without changing the Q signal, we get a resultant wave with a phase of 135°. See Figure 3 below.

Figure 4 shows that if we invert both signals, we get a resultant wave at 225°.

Finally, if we only invert the Q component, we get a resultant wave at 315°. See Figure 5.

As long as the amplitudes of the I and Q waves are identical (can you sense the foreshadowing?), these are the four possible I/Q combinations and their resulting phase shifts. These serve as the basis for 4-QAM (which is effectively the same as the QPSK modulation method used in 802.11).
The number preceding “-QAM” refers to the number of possible symbols used in said version of QAM. So, with 4-QAM, there are four possible symbols. To determine the number of bits that can be mapped to each symbol, you can use the following formula, where M is the number of possible symbols:
$$ \large {\color{Red} bits\: per\: symbol}= \log_{{\color{blue} 2}}{\color{goldenrod} M} $$Don’t be intimidated. This formula is just asking, “What power of 2 can I use to get M?” We use 2 as a base because we are using binary numbers, and each bit can only hold one of two values (0 or 1).
So, with 4-QAM, this formula would become:
$$ \large {\color{Red} 2}= \log_{{\color{blue} 2}}{\color{goldenrod} 4} $$We know that 22 equals 4, so each symbol in 4-QAM can be mapped to 2 bits.
I’ll cover 4-QAM in more depth in Part 2!
Wave images created with EMANIM:
Szilágyi, András (2019): “EMANIM: Interactive visualization of electromagnetic waves”. Web application available at URL https://emanim.szialab.org